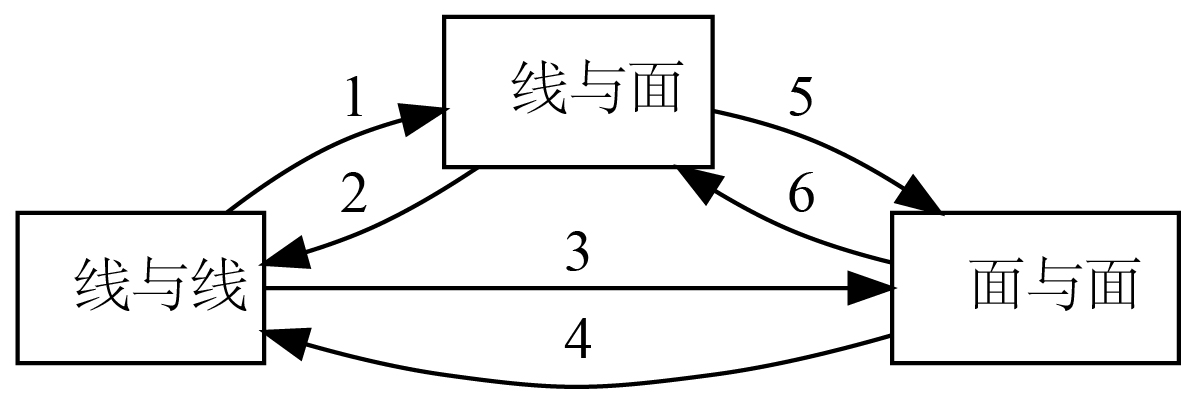
垂直

$1$

1. 定义：$\forall m \subset \alpha,l \perp m\Rightarrow l\perp \alpha$
2. 判定：$m\subset\alpha,n\subset\alpha,m\cap n\neq\varnothing,l\perp m,l\perp n\Rightarrow l\perp\alpha$

$2$

$l\perp\alpha,m\subset\alpha\Rightarrow l\perp m$

$3$

$m\subset\alpha,n\subset\alpha,m\cap n\neq\varnothing,l\perp m,l\perp n,l\subset\beta\Rightarrow\alpha\perp\beta$

$4$

$\alpha\perp\beta,\alpha\cap\beta=l,m\subset\alpha,m\perp l,a\sub\beta\Rightarrow m\perp a$

$5$

$l\perp\beta,l\subset\alpha\Rightarrow\alpha\perp\beta$

$6$

$\alpha\perp\beta,\alpha\cap\beta=l,m\subset\alpha,m\perp l\Rightarrow m\perp\beta$

三垂线定理

1. 定理：$l$ 是平面 $\alpha$ 的一条斜线，$l$ 在平面 $\alpha$ 上的射影为 $m$ ，$a\subset \alpha $ ，$a\perp m\Rightarrow a\perp l$
2. 逆定理：$l$ 是平面 $\alpha$ 的一条斜线，$l$ 在平面 $\alpha$ 上的射影为 $m$ ，$a\subset \alpha $ ，$a\perp l\Rightarrow a\perp m$