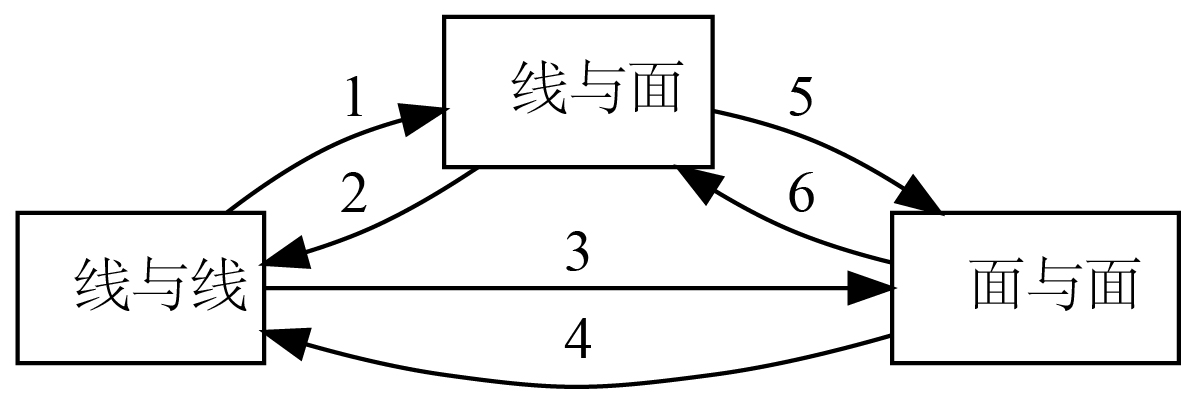
平行

$1$

1. 定义：$l \cap \alpha = \varnothing\Rightarrow l//\alpha$
2. 判定：$l \nsubseteq \alpha,m \subset \alpha,l // m\Rightarrow l//\alpha$

$2$

$l//\alpha,l\subset\beta,\alpha\cap\beta=m\Rightarrow l//m$

$3$

$l\subset\alpha,m\subset\alpha,a\subset\beta,b\subset\beta,l\cap m\neq\varnothing,a\cap b\neq\varnothing, l//a,m//b \Rightarrow \alpha//\beta$

$4$

$\gamma\cap\alpha=l,\gamma\cap\beta=m,\alpha//\beta \Rightarrow l//m$

$l\perp\alpha,m\perp\alpha\Rightarrow l//m$

$5$

$l\subset\alpha,m\subset\alpha,l\cap m\neq\varnothing,l//\beta,m//\beta\Rightarrow \alpha//\beta$

$6$

$\alpha//\beta,l\subset\alpha\Rightarrow l//\beta$